Simon Gronlund is earning his Master of Science in Computer Science at the Royal Institute of Technology, Sweden, as an adult student. He also teaches Java and computer-related courses on a senior high school level. When he isn't tampering with his Warp 4 PC, he spends his spare time with his two boys and his wife.

Into Java, Part 6

A short recall on recursion. Last time we wanted to go through text strings, one line after another, to find or replace a particular string. Since we never know if there is no, one or more occurrences of the particular string we are looking for, we have to continue with the rest of each line after we found an occurrence. Then we made a recall to the same method with the remainder of the string.

On the way back, winding ourselves back to the original caller, the complete string was reassembled again, but now with the string searched for marked or replaced. If you didn't read the last Into Java column, please turn to that column first.

The way we used recursion last time is the simplest way of recursive calls, and hence most easy to understand. Today we will add to it the normal way of recursion, when there is not only one but several call-backs each turn. So, fasten your seat-belts.

Extended recursion

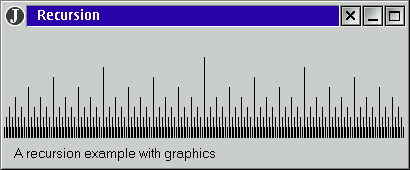We will build ourselves an application that will show us some vertical rulers of different heights. As we can see, the middle ruler is the highest one. Then at the exact middle from that one to the ends, the second highest rulers show up, two of them. And at the exact middle of the quarters we got the third highest rulers show up, four of them. And so forth. How did we manage that?

Obviously the middle ruler is drawn solely, but it looks like the following rulers are drawn in parallel, the next highest, the third highest, down to the lowest rulers. Is it so? Let us look at the code (and once again some parts are not yet explained). The recursive method is the drawRuler that receives some initial values and a start level. Unlike the former recursion we studied this method does not need return anuthing.

Recall that recursion always uses the trivial case as an "am I done now?" test and the first line is a check for the trivial case, and if so nothing is done and the method abruptly exits. Else we compute the mid value, based on the given left and right values. Then we continue with a new operation, basically we draw a line from one (x, y) position to another (x, y) position, the latter y based on the given level. This level will in our case start at 8, and recall that the coordinate system of computers is upside down.

After that the recursive calls to drawRuler itself are made, both almost at the same time. The first call seems to be the left side ruler, and the second call is the right side ruler. The level is appropriately reduced by one within the recursive calls. But is this idea of the work actually the truth?

private void drawRuler(Graphics g, int left, int right, int level) { if (level < 1) return; int mid = (left + right) / 2; g.drawLine(mid, 110, mid, 110 - level * 10); drawRuler(g, left, mid - 1, level - 1); // left drawRuler(g, mid + 1, right, level - 1); // right }

No, it is not the truth, but it can be and really is, a perfect way of imagining how the workload is done. First the middle ruler, then the next highest rulers at the middle of each side, continued with the third highest rulers at the middle of each quarter delimited by the existing rulers, and so forth.

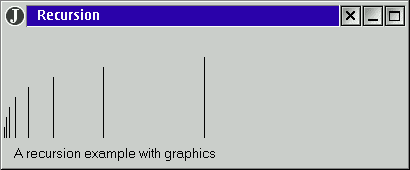The image to the right shows what happens if you erase the last line of the drawRuler method. The middle ruler is drawn, the second highest ruler and down to the lowest one every ruler to the left is drawn. But no one ruler to the right, obviously since the last line of the code is erased. But this gives us a clue of what is happening inside the computer, too.

Even if the last line of the method is there the first eight rulers drawn will look like the image to the right. Since each recall to drawRuler takes us more and more to the left until the expected level is reached, no call is ever made to a right ruler. The first time we ever enter the last line of the method is when the leftmost ruler is completed and drawRuler returns at the trivial case. Then we draw a ruler to the right, but still the level will be at the lowest possible so no more rulers will be drawn.

The method returns up the second lowest level possible only to find that the last line is still not done so it now dives to the right. Only to have to go the left. Yes, I see this is not easily explained <grin>. I will then use a white board sketch.

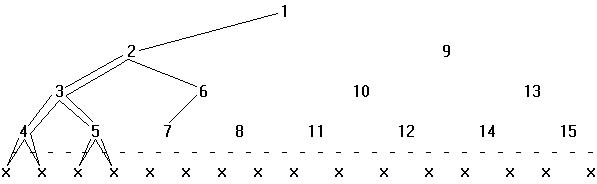
Here are less rulers and they are numbered from one and upwards as they are drawn. It is easily seen that we are going leftward until we reach the bottom level, there we try to go one step further but find the trivial case and is returned to number 4. In number 4 we try to go to the right, but again find the trivial case and end up at 4 again, with nothing more to do. Hence we return to the method that called number 4, that is number 3.

In number 3 there are one line undone, the last one that sends us to the right, which will be number 5. In number 5 we draw another ruler and then try to go to the left--the trivial case is found--and we try the right side--again the trivial case--so we return upwards to number 3. There we find that we are done with number 3, so we return to number 2, which will send us down to number 6, that draws that ruler and then turns to left, the "left" code line. This way we swirl around until we finally reach number 15 and wind ourselves up to number 1 and find that now we are done with this recursive lesson. Thirtyone calls were made to drawRuler to draw these fifteen rulers, of which 16 were calls to the trivial case.

To the code enclosed I have added a few lines (the lines with variables test and max) that you may use to see how the bars are drawn. You may change max to different values and thus the recursion will stop after that many turns. If you increase max by one each time, you will clearly see what happens, unfortunately you have to recompile the class each time.

In spite of how the work is actually done within the computer, many programmers think of the different levels being drawn at the same phase, and then the next level. Either way the result will be the same. It doesn't matter how many lines there are making recursive calls, there is always kind of a thread that you may follow that will sketch a tree upside down. As an exercise you can compute the different values for mid, left, right and level using the sketch. Try to solve the exercise with starting values as left=0, right=32 and level=4.

Graphics

As long as we only use common building bricks like JFrame, JPanel, JButton etc., we never need to worry about Graphics since that is handled automatically within those classes. But if we like to do something on our own, like we did above, we have to know about one particular method that we have to use, the paintComponent method. And we briefly have to know what Graphics is, since it shows up from time to time.

paintComponent

Back in Java 1.x times, without Swing, you maybe used Canvas as a painting surface. Please, forget about that and make use of the much more powerful Swing components. That way you will avoid flicker, you will get buffering and some other useful improvements, too. In fact, if you try to combine the old style with Swing you might get into serious trouble, not necessarily, but stay warned.

Never mind, we wanted to draw something extra on the surface of such JComponent and thus we have to add instructions to the paintComponent of the item we choose. Hence the code will look like underneath.

class Rec extends JPanel { public void paintComponent(Graphics g) { super.paintComponent(g); drawRuler(g, 0, 400, 8); g.drawString("A recursion example with graphics", 10, 130); } private void drawRuler(Graphics g, int left, int right, int level) { ... } }

We see that this class extends JPanel, only to use it as a surface to paint on. The next thing we see is that paintComponent is making a call up to the ancestor, using super and handing that Graphics variable g along. Never forget that! How should the JPanel itself be updated if you take this line away?

But hey, what is that Graphics g then? Consider Graphics a tool box, or a collection of methods to draw lines, as we do, rectangles, polygons etc. Hence g is a reference to that collection and you may use it to get in touch with every method mentioned in the Java API under java.awt.Graphics. So, when we read g.drawString("A ..., we can look up drawString and find that it "Draws the text given by the specified string, using this graphics context's current font and color. The baseline of the first character is at position (x, y) in this graphics context's coordinate system". The g referred to Graphics that included this useful method.

Where did g come from initially? The truth is that we never did much to instantiate that g, but the JVM creates a Graphics object each time an application using GUI starts, and sends a reference, g, of that object to every component that has to be made visible. If we don't have to draw something of our own we never bother our minds with that g or the paintComponent, but still it swirl around making the app visible.

What do drawRuler(g, 0, 400, 8) do? That is actually the first call to the recursive method drawRuler we have discussed. We pass the variable g as well as the starting parameters. When every recursive call is done we come back and executes the drawString and then we are finished.

The only remaining code is the driver that makes everything run. You will find it enclosed at the end of this column. Please feel yourself free to experiment with the Rec class and try other objects from the Graphics class. You might use any drawX and fillX method you see there. If you would like to use colors, you can look up Color. You might write g.setColor(Color.red) or g.setColor(new Color(0, 0, 255)) for instance. Or try different fonts, found in Font. Play around as you like to.

Summary

If you would like to draw things yourself, you first pick a JPanel and then you have to override the paintComponent method of that class. First line should always be super.paintComponent(g). Then you use the reference through g to reach the collection of methods found in Graphics. We will return to this topic in a future column.

Complete code to Recursion.java and to Rec.java