

16 January 2001
 Simon Gronlund is earning his
Master of Science in Computer Science at the Royal Institute of Technology, Sweden,
as an adult student. He also teaches Java and computer-related courses at the college.
When he isn't tampering with his Warp 4 PC, he spends his spare time with his two
boys and his wife. Simon Gronlund is earning his
Master of Science in Computer Science at the Royal Institute of Technology, Sweden,
as an adult student. He also teaches Java and computer-related courses at the college.
When he isn't tampering with his Warp 4 PC, he spends his spare time with his two
boys and his wife.
If you have a comment about the content
of this article, please feel free to vent in the OS/2 eZine discussion
forums.
|

|
Into Java, Part 13
How amazing, this installment numbers
thirteen and the columns now span over three years and two milennia. Now even the
puritans can agree on that, December 31th last year the second millenium ended and
the third one started. Time is flying away too fast to imagine, but the computer
business seems to keep in pace.
This time we will have a discussion
on data structures. Fred Brooks once wrote: "Show me your <code> and
conceal your <data structures>, and I shall continue to be mystified. Show
me your <data structures>, and I won't usually need your <code>; it'll
be obvious."--The Mythical Man-Month, Ch 9.
Yes, data structures most often is
the heart of your implementation, a good choice will reward you several times over,
a bad choice and you will regret it over and over again. That is since data structures
quickly becomes the skeleton of your application, and as your skeleton hardly is
replaced, data structures are hard to replace.
I have said before that good and
thoroughly modeling is essential to programming, using papers and a pencil. But
how to include the data structures in that planning. This column will entirely discuss
that topic.
Mathematics and computer science
go hand in hand, so even this time. Hence I will cover a little math, but do not
be scared off, I will not go too deep into that. Further computer hardware works
in its own way, and we have to be aware of a few things because of that.
The developers at SUN seems to have
read their math before implementing the Collections framework in Java 2 (see note), hence we start with a few math notations, then how these
are implemented in data structures. You may also read the interesting pages in the
Java API v 1.2 or later, X/docs/guide/collections/overview.html there you have to substitute X with your
folder, or a URL to SUN's site.
|
The math
A set is simply
described as a collection of elements that need not be ordered. The Set interface
used in Java follows the hard restrictions that math states, no two equal elements
are allowed. We may think of an alphabet (unordered though), no two equal letters
are allowed. On the other hand we are not forced to put every letter we know about
in the set, I would hardly put umlaut letters in an alphabet showed to English readers,
though I know these letters very well.
The Java
Set is an interface that
specifies quite a few methods that a set should have, but Java has a class of the Set interface
ready to use, the HashSet. Further Set is implemented by the
SortedSet interface, that
in its turn is implemented by TreeSet. (Please do not be worried by the many class
names, we will look to some of them, and the remaining ones you may look up in the
Java API.)
A list is on
the contrary an ordered collection allowing duplicates. Ordered does not imply sorted,
only that we know that item "X" is located at index 45, and maybe another
"X" at index 201. Or wherever. Only think of a lined up scout patrol,
a straight row there everyone has his/her place in the line, though no need to line
up by names and two Bill Smith is allowed.
Java uses the
List interface of methods
that give us precise control over where we store your objects. We have already used Vector that
is an implementation of List, but there are also LinkedList
and
ArrayList to chose from.
Furthermore, map
that is more of a function, as sin(60°) maps to 0.5, or telephoneNumber(Gronlund,
Simon) maps to 1234567, a key maps to a value . Since a
discrete key maps to a discrete value no two duplicate values are allowed. A map
is not considered ordered, no straight line of elements is found, nor are they promised
to be sorted though some Java classes that follow the
Map interface are sorted.
HashMap, Hashtable and WeakHashMap are
some classes that implements the Map interface, as well as another interface, the SortedMap that
is implemented by TreeMap.
These three fields matches the major
interfaces of the Java Collections framework. Java Collection
also has the SortedSet,
but we will wait with that until another Java column.
root
|
|
node
/ \
/ \
/ \
node node
/ \ / \
/ \ / \
node leaf node leaf
/ \ / \
/ \ / \
leaf node leaf leaf
/ \
A binary tree,
two branches out of each node
|
|
Finally, I will mention a very useful
structure, namely a tree , named so because of its shape. Think
of a tree upside down, the root is topmost and the branches grows from the root
to the leaves at the end of each branch.
Though many trees used are binary,
they have only two branches each node, there are other flavors too. I have used
trees with as much as 28 branches each node, but then we are not really discussing
ordinary trees and we will leave that for now. Why trees are that popular will be
explained in a few minutes but they are, and then binary (and ternary, i.e. 3-branched)
trees are the most popular ones.
Trees are a big area of research,
included in graph theory, and many interesting results have been found by computer
scientists, tailored, used and adopted in the computer industry. Of course trees
have found their way into the Java Collection, for example TreeMap, that is a well thought out piece, and its
cousin TreeSet,
that is something in between.
Before we continue I will introduce
a few words, and their meaning. A node is a point in a tree
or a list that we may walk to, following a reference. It has at least one reference
to it and may have one, two or more references out. Most nodes are made up by a
small class, a helper class, that holds the references to 1/ the data, 2/ other
nodes whereof one may be the parent node, and 3/ some internal information. Nodes
are used on other data structures than trees and works almost the same wherever
they are found, as the private and invisible class Entry
inside
LinkedList is a node.
The non-value
null is used when there
is no reference to another node, and if every variable that should point downwards
to another node is null,
this node is considered a leaf, it has data but no legal
references.
Accordingly child
and parent are used, the child is a node of this
node, and a parent is this node's superior level node. These terms may be
fuzzy when complex structures are used and no obvious levels or ancestors are seen.
The root is often
used as the main class of the particular data structure, and holds a reference to
the first node but most often no data. The root holds most of the convenient methods
that are used on the data structure, such as add, remove,
contains, etc. Since Java
gives us many prefabricated methods we may perhaps be happy with numerous of them.
Finally, the way you need to go from
the root to a specific node is called path , but in fact any
way you need to go in a graph such as a tree is called a path.
Computer basics
From the very beginning technicians
have been storing data as bit by bit, normally thought of as
1 and 0, and implemented as distinct electrical values, such as +85 mV and
-85 mV or alike. The bits are held together as a byte,
now a byte is thought of as an eight bit byte. Do not confuse a byte with the 32
bit (or 64 bit) compound that is called a word. A word is set
up by several eight bit bytes.
Type
|
Size
|
Range (approximately)
|
Floating-point numbers
|
double
|
8 bytes
|
±1.7977E+308, 15 significant
digits
|
float
|
4 bytes
|
±3.4028E+38, 6 significant
digits
|
Integer numbers
|
long
|
8 bytes
|
±9,223,372,000,000,000,000L
|
int
|
4 bytes
|
±2,147,483,000
|
short
|
2 bytes
|
32,768 to 32,767
|
byte
|
1 byte
|
-128 to 127
|
In one of the first parts of this Java
programming series we looked at the basic data types, let us remind ourselves. First
we can see that Java is already prepared for easy handling by 64 bit CPU's, as double and long is 8 x 8 = 64 bits
long. But the smallest compound, the byte, is one eight bit byte only.
Shall we now think of how data is
stored in the computers working memory (RAM). That is not hard to explain, whenever
the CPU reads an instruction that tells it to store a variable (let us say an int)
it needs two parts, the data and the address in the memory. The latter is made up
by the compiler (and the JVM when using Java) in conjunction with the operating
system (OS), and the very smallest area to address is an 8 bit byte.
When the CPU executes that instruction
it accesses the RAM at the told address and stores the data there. Another variable
may later be stored, and is then stored at another address. The more variables stored
the more addresses are used, but there are no distinct rule where these addresses
may be located. Hence they may be scattered around, or accidentally be grouped together.
But no one variable knows the location of the others, they are no part of a data
structure.
Arrays--the simplest structure
A long time ago the array was found
as a good way to collect related variables together. We may for example measure
the temperature each hour and need a way to store these values, then a 24-element
array is suitable, one array each day.
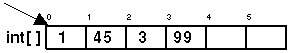 An array is simply several
variables in a row, the compiler fixed some kind of code that orders a line of consecutive
variables as seen in the image and the OS manages that. The advantage from this
is that now we only need one address that points to the beginning of the array,
held by the reference.
An array is simply several
variables in a row, the compiler fixed some kind of code that orders a line of consecutive
variables as seen in the image and the OS manages that. The advantage from this
is that now we only need one address that points to the beginning of the array,
held by the reference.
 The elements is found as the result
from add up the reference with the offset, the first element having zero offset.
Here is the reason why arrays, Vector and other data structures start at number
zero, the offset is zero at the first element. Hence we now can get to "99"
by adding 3 to the reference, as int answer = myIntArray[3] where myIntArray holds the reference.
The elements is found as the result
from add up the reference with the offset, the first element having zero offset.
Here is the reason why arrays, Vector and other data structures start at number
zero, the offset is zero at the first element. Hence we now can get to "99"
by adding 3 to the reference, as int answer = myIntArray[3] where myIntArray holds the reference.
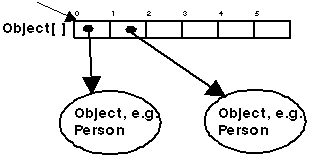
Arrays may be used not only with
basic data types as byte, short, int, long, float or double, yes, in fact, with
boolean as well. But we
can add any kind of objects to them; MyClass[], Integer[]
or
Object[] are legal, as any
class is. If different kind of objects have to be stored in the same array, then
use the cosmic Object class
as the type.
Normal array operations are as follows.
Please note that arrays have a convenience variable named
length that is read directly
and not through a method. Also note that arrays always are accessed with square
brackets; [ ].
byte[] byteArray; // declaration only
// later, initiation with size 9
byteArray = new byte[9];
/* declaration and initiating of an array of size 17 */
short[] shortArray = new short[17];
/* and using Object, size 5 */
Object[] objArray = new Object[5];
/* declaration and initiating of an array, size becomes 5
* and the elements 1, 2, 3, 4 and 5 are stored in it */
int[] integerArray = {1, 2, 3, 4, 5};
/* and using String, size becomes 3 */
String[] stringStore = {new String("Alpha"),
new String("Beta"), new String("Gamma")};
/* assigning values to an array */
shortArray[0] = 4;
shortArray[17] = 12; // illegal, indexes are 0 to 16, see above
shortArray[10] = 125000; // illegal, >32768, a short's limit
stringStore[0] = new String("Omega");
stringStore[1] = new StringTokenizer("Delta"); // illegal
// StringTokenizer is not a String
/* getting values from arrays */
int x = integerArray[0]; // x will be assigned 1
int y = integerArray[5]; // illegal, index out of bounds
/* and getting objects */
String tempStr = stringStore[2]; // access to Gamma
/* finally try this */
for (int i = 0; i < integerArray.length; i++) {
// set a value in integerArray
integerArray[i] = (i * i); // square of i
}
for (int i = (integerArray.length - 1); i >= 0; i--) {
// get values from integerArray
System.out.println("i = " + i + " and i*i = "
+ integerArray[i]);
}
/* finally set and get values from the objArray */
objArray[0] = new String("zero");
objArray[1] = new Integer(1);
objArray[2] = new Double(2.0);
objArray[3] = new Character('3');
String newStr = (String)objArray[0]; // cast is needed
Integer newInt = (Integer)objArray[1];
...
|
|
Using arrays is convenient, and as
they are very close to the computer hardware environment they are efficient and
do not cause that much overhead. Why not only using arrays then?
The first limitation is the length
of an array. The length can not be changed dynamically, and that is true for every
kind of computer and OS, always. If any programming language looks like having such
a feature, that is a fake, beneath the surface there is some kind of functionality
fooling us around. That is clearly understood when considering how an array is laid
out, the OS gets an order for, let us say, an int sized array with 10 elements. That is 10 by
4 bytes (an int needs
32 bits and 4 bytes * 8 bits = 32 bits) resulting in 40 bytes in a row. Maybe next
step for the OS is an order for one long sized variable (8 bytes) and by an unlucky
coincidence it is placed at the very next free address after the array. Thus the
array can not grow into that spot.
Growing an array is a simple matter
of ordering a new one, that much longer as we like it to be. The OS will give us
a new and empty one and we then do a simple copy and paste from the original to
the latter one using arrayCopy of the System class. Finally we simply leave the original
to destruction and soon the OS will recycle the address area. Exactly the same operation
is performed upon shrinking the length. These operations are of course time consuming
and considered inefficient. Still many Java classes are based on simple arrays,
as Vector uses
an Object array
and performs the operations just explained when necessary.
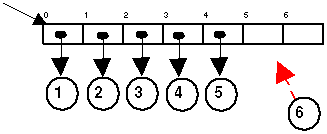 Else, normal actions on simple arrays
are performed efficiently and with no hassle. They are easily understood and not
hard to implement. Since Java hides the hazards with pointers and pointer arithmetic
the work is a breeze, as the add method show us in the left hand image. We simply keeps
track of the last index used and add the next element to the next index.
Else, normal actions on simple arrays
are performed efficiently and with no hassle. They are easily understood and not
hard to implement. Since Java hides the hazards with pointers and pointer arithmetic
the work is a breeze, as the add method show us in the left hand image. We simply keeps
track of the last index used and add the next element to the next index.
The next inconvenience occurs when
we implement the remove and insert methods,
let us discuss them to some extent. The simple removeLast
and
insertLast are disregarded
as they are implemented as decrementing the size variable and add
respectively.
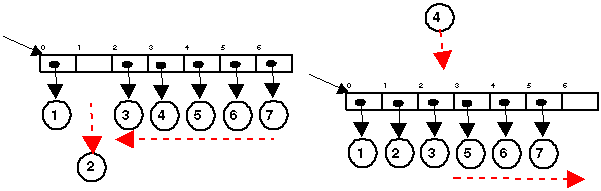 Consider the left
part of the image, we remove the second element. Remove is clearly different from
assigning the second box another object, remove will leave an empty box, and empty
boxes, how would you like to keep track of them? You don't, you have to move every
element to the right of the empty box one step leftward. Again that is time consuming,
more time is spent the more leftward the removed element was located and the longer
the array is.
Consider the left
part of the image, we remove the second element. Remove is clearly different from
assigning the second box another object, remove will leave an empty box, and empty
boxes, how would you like to keep track of them? You don't, you have to move every
element to the right of the empty box one step leftward. Again that is time consuming,
more time is spent the more leftward the removed element was located and the longer
the array is.
Exactly the same argument is valid
with insert, we have to move every element to the right one step rightward, finally
we can add the new element in the obtained empty box. Both methods have the worst
case scenario of T( n ) where n is
the number of elements in the array and T is the time spent on each iteration (computer
scientists use the term big-O, but we will leave that). The best case
is T( 1 ) since that is simply removeLast or insertLast discussed earlier. The average case
is T( n /2 ) since the average case is the middle element
being changed. To that we most of the times have to add the time to find which index
the element we will remove has, or the one to insert is to be given, which doubles
the time.
Hence arrays and classes that are
built on arrays are good for simple data structures without too many remove or insert.
Order an array of the expected length from the very beginning, thus avoiding too
many arrayCopy operations.
Many delicate implementations are built on simple arrays. On the other hand many
applications suffer from being built on arrays that do not scale well or suffer
from time consuming operations.
Linked lists--the solution to insert and remove
cons
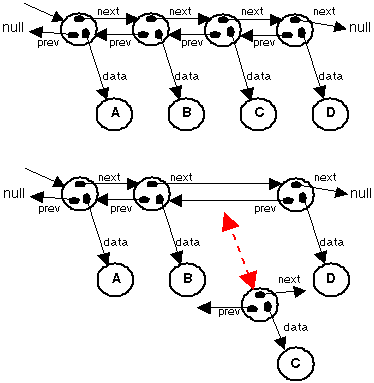 As the
problem with insert and remove came from the time spent on
arrayCopy, shuffling elements
left- or rightward, we would like a data structure that do not need these operations.
A linked list is the answer. Think of nodes linked, or chained, together as the
uppermost image part shows.
As the
problem with insert and remove came from the time spent on
arrayCopy, shuffling elements
left- or rightward, we would like a data structure that do not need these operations.
A linked list is the answer. Think of nodes linked, or chained, together as the
uppermost image part shows.
The root knows at least the first
node, many times it also knows the last node. If the list is single linked only
the next reference
is used and we can only traverse the list in one direction, going forward. If the previous reference
is used we have a double linked list and can traverse it both ahead and back, as
the image shows. The Java LinkedList is a double linked list, also knowing its
last node, but note that it is the base class that knows the start and end of the
chain, the nodes themselves know only the next and previous, as well as their
data.
Now look at the lower part of the
image, an insert (or
is it a remove?)
is to be done. The methods need to change the next and previous references to include (or exclude) the "C"
node, that is all. Okay then, that is a little tricky but it is nothing more than
switching references so that the "C" node's
next will refer to the same
as the "B" node does, then changing the next
of "B" to refer
to the "C" node (note that we talk about the nodes and not the data, but
use the data as a label in our discussion). Likewise we set the
previous of the "C"
node to reflect the "D" nodes reference, and then changes the previous of
the "D" node to refer to "C". The remove is analogous to this
procedure.
Hey presto, now both insert and remove
will only take T( 1 ) since there is no shuffling elements around. The
different objects may be stored anywhere in the computers RAM, still the variables
refer to the correct objects. But are there no drawbacks?
Of course there are some drawbacks
and some shortcomings, every data structure suffers from limitations and you are
the one to chose the best compromise. Handling arrays are efficient in many ways,
the data is stored tight to each other and hence derive advantage from the "read-ahead"
that most OS's use, from the cache mechanism and a few more benefits. Instantiating
objects eats time, we never know were they actually are stored (we do not need to,
but the tight data storage is lost) and there is some overhead with objects.
Anyway, quite a few times we decide
that we can live with these shortcomings, the usefulness outweighs the shortcomings.
But still the worst thing is that methods like contains(Object)
or
remove(Object) still have
the same best, average and worst cases. How come? Since these methods have to iterate
each node until the correct data is found. There is no shortcut to find the correct
one, each one has to be examined with a fail or pass.
The same arguments hold if we like
to maintain a sorted list (Java LinkedList do not support sortability, but we are
free to implement such a list). To sort a "Y" after "X" we have
to find "X", and that takes T( n /2 ) on average.
Lists are mainly used to hold queues,
methods like addFirst and removeFirst performs
well and the overhead is ignorable in these cases. Unordered collections perform
well, except from searching them.
Now we have tracked down to "how
to sort into a sorted data structure?" So far we have found no good data structure
to maintain a sorted collection and perform operations on that collections efficiently,
though the linked list is much better than an array. Any kind of array or list suffers
from being linear, it is traversed ahead or backwards. May the tree structure be
the solution?
The binary tree
Straight to the point, the tree is outstandingly
fast with insert, remove, contains(Object) and whatever we like to process on it. Trees
belong under set discussed as the first of three math definitions,
a set do not allow duplicate objects stored.
If we consider a huge telephone database,
there is not two objects referring to the one individual. If so, the database
will soon get unstable and when we update one record the other one will still be
reflecting old data. Fulfilling these requirements of no duplicates we can start
with instantiating MyTree, that is we get ourselves a root to the still not yet
created first node.
We pick the first individual and
instantiate an object from the data read. Then we pass the data to
add(Object) that creates
a new node referring to the object. Since it is the first node added to the tree
it simply becomes the first node the root refers to, and the node itself have only
two null-references
as the left and right variables.
The value of the data is so far irrelevant.
Next individual is instantiated and
the object is passed to add(Object) that creates a new node. But since it is not
the first node added to the tree we have to find out if it is to be placed to the
left or the right from the existing node, using the left
or
right child of the first
node. To make that comparison our object must be able to answer a compare-to
question, that is, we have to have a method named compareTo. That method is outlined in the Comparable interface
that we have to implement in our class if we are using any of the Java Collections'
classes that support sorted collections.
compareTo(Object)
A class implementing the Comparable interface
only has to implement the single compareTo(Object) method. Think of us standing in an object,
the this object.
We receive another object, named other, and we have to answer to the question "is
the other object lesser than, equal to, or bigger than your object is?" Look
at the limited code below.
public class MyShoes implements Comparable {
short shoeSize;
public MyShoes(short size) {
shoeSize = size;
}
public int compareTo(Object other) {
MyShoes temp = (MyShoes)other; // a cast
return (int)(temp.shoeSize - this.shoeSize);
}
}
|
|
Naturally other things may guide the comparison of shoes than
only the size, but the lesson is the same. We return a negative int value if we
are less than the other object, zero if we are equally sized, or a positive int
if we are bigger than the other. For example, the String
class performs a true lexicografically comparison, taking
upper and lower cases into account. How we compare objects is up to us, but the
comparison has to be done if we like to maintain a sorted collection.
Continuing with the adding to the
tree we chose left or right, less
than to the left, else to the right (equal to is not allowed). This time we imagine
we got the left choice. Reading the third individual results in the next node, which
data shall be compared with the first node's data, left or right. If it is to the
left we continue with comparing the new node with the left node's data, the second
node made. That is, we have to go one step deeper to make another comparison. Else
we can simply add the new node as the right child to the first node. I will try
to illustrate it.
I. root II. root III. root IV. root V. root
| | | | |
"Mike" "Mike" "Mike" "Mike" "Mike"
/ / / / \
"John" "John" "John" "John" "Simon"
/ / \ / \
"Chris" "Chris" "Len" "Chris" "Len"
|
|
For example "Chris" is
first compared to "Mike", then to "John" and is then set as
the left child of "John", but "Len" is lesser than "Mike"
but greater than "John" and was set to the right of "John".
But this tree does not look sorted at first sight, does it? Reading a tree in order
we first have to find the leftmost node, in our case "Chris" that also
is the first name of this collection. From that node one step up to the parent and
reading that node, "John", which is correct. Then down the right child
one level, and try to find the leftmost node again (which can be a few levels down
actually). This time there is no leftmost node of that child so we read the node,
"Len", again correct. Try to go down to the right, but there is no right
child. Upwards, but we have read John so we leave him and head for his parent, "Mike",
that is correct. Does "Mike" has a right child? And does that child has
a leftmost node downwards? "Mike" has a child, "Simon", which
has no children. We are done.
The rules seems to be,
-
try to go left
-
if possible, go there and continue from
1
-
else, continue with 2
-
read this one
-
try to go right
-
if possible, go there and continue from
1
-
else, do nothing, we will recursively
return to your parent
and we will get the elements in a sorted
way. The recursion is the tricky part to follow, but remember that the computer
remembers were it left off for the child, and the parent will continue executing
the code were it left off for a while. Since there are such advanced and good Java
classes prefabricated I will not give any code here, only links to the recursion
installments, Java V and Java VI
that explains the mechanism used.
Now, why use such non trivial structures
as trees? Since they give an outstanding performance hit on sorted collections,
any kind of look-this-up operation is done fast and quickly, if the object is in
the tree it is found that snappily, or it says "the object is not found".
Insert-this is executed as quickly. How come?
Here a little more math is needed.
The example above is not that big, but still it shows that each level double the
number of nodes, the zero level is only one node, the first level is two of them,
"John" and "Simon". The second level is already having place
for four nodes, though only two is used. The next level will have eight, the next
sixteen and so forth. Clearly we see n = 2h
where n is the number of nodes possible, and h is the
height of the tree, the number of levels used, having the first node at level zero.
But that is not the whole truth, since each node at each level also may be used
and that gives a much better sum of nodes, an expression that reads n = 2(h+1) - 1.
Such expressions grow rapidly, only
ten levels, including the zero level, will give room for 1,023 nodes, and 20 such
levels will gladly accept more than one million objects. Hence I can promise that
a telephone number database with one million individuals will never suffer from
more than T( 20 ), or more precisely put, the worst case will be T( h ),
where h may be computed by h = lg( n ).
But this is not completely true, since that is based on the assumption that all
trees grow balanced and equally, which is not a fact. Still the Java classes that
support sorted trees are that close to the lg( n ) that we
can forget about the difference.
There is simply no other data structure
giving us this splendid performance with that little implementation effort, we can
find any person of that one million person telephone database within 20 comparisons,
remove him or simply read the data. An insert is made equally fast. Is there any
drawbacks then?
Yes, of course there are drawbacks,
didn't I told you? <grin> So far we assumed that the input to the tree was
picking individuals randomly, but consider moving from one ordered and sorted data
structure, that have served for a while, to a tree. We pick the first individual,
"Aaron", then comes "Abel", "Abdul", and so forth.
"Aaron" will of course be the first and topmost node, but "Abel"
will surely be bigger than him and set as the right child. So will "Abdul",
"Abraham" and every other individual be, set as the right child to the
right child, no one will ever be placed to the left. The result is again a linked
list and the last person will be that many levels away from the root.
Apparently a tree is not suited for
that kind of input, but else it works nice. There are naturally several ways to
solve the dilemma, pick the objects at random and watch out for picking the same
twice and not to forget someone, or start at the middle and then recursively pick
the elements as in the recursions discussed in installment
6. Or any other method of your mind.
To avoid heavy unbalance in trees
something named the red-black tree was invented and implemented, in fact it is used
by Java TreeMap.
It promises that no path is more than twice as long as any other path, thus giving
us a reasonable balanced tree. Consider that the more precise balancing we require
the more overhead it causes the tree's balancing mechanism. And there is not much
difference between 10 and 20 levels, not compared to the up to one million look-ups
on a list or array, or 500,000 on average.
The map, hash and table
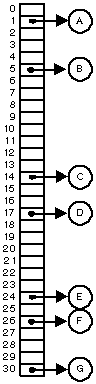
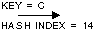 Still
the data structures we have examined do not have T( 1 ) at look-ups. Is
there a way to get such good results? Yes, the mapping concept gives that performance.
Consider having an array with 30 empty indexes, and a function that takes the object,
or a key, and computes something (a pseudo-index) that can be mapped to an index
of were to put the object. If that function promises to always compute the same
pseudo-index from equal keys, and also to spread these pseudo-indexes equally along
over a fix length, then any look-up or insert will execute with T( 1 ).
This data structure is mainly called hashtable or hashmap since we hash
the pseudo-index, called the hash value, from the key. That hash value is mapped
into an index of the array and the object is put in a table or a map. Are there
any drawbacks <grin> ?
Still
the data structures we have examined do not have T( 1 ) at look-ups. Is
there a way to get such good results? Yes, the mapping concept gives that performance.
Consider having an array with 30 empty indexes, and a function that takes the object,
or a key, and computes something (a pseudo-index) that can be mapped to an index
of were to put the object. If that function promises to always compute the same
pseudo-index from equal keys, and also to spread these pseudo-indexes equally along
over a fix length, then any look-up or insert will execute with T( 1 ).
This data structure is mainly called hashtable or hashmap since we hash
the pseudo-index, called the hash value, from the key. That hash value is mapped
into an index of the array and the object is put in a table or a map. Are there
any drawbacks <grin> ?
Collisions, when it happens that
two unequal keys gives the same index (rare but possible), cause a drawback that
gives us some headache, we have to take care of the situation and that will increase
the time consumed somewhat. Another drawback is the same as with arrays, if the
table grows to much we have to lengthen the array. But we cannot use the speedy arrayCopy,
instead we have to re-hash (re-map the hash values) of every object since now we
have more indexes to chose from and the look-up function will map the hash value
onto that many indexes, not onto the previous length. This re-hashing wastes a lot
of time, but can be prepared for by giving the table a good initial size.
Also, to avoid too many collisions
we must waste some memory, some unused memory. The benefit is that the mapping will
be wider or broader and thus the chance is better that a collision will not occur.
It is not correct, but simple, to say that there are more free slots to pick from.
Incorrect since the mapping does not use the free/not-free state in its calculation
of the index. But it is simple since the more free slots there are the better chance
to get a free one. Normally a hashtable uses a load factor of
0.75, it wastes at least 25% memory space, "a good tradeoff between time and
space costs" as the Java API states.
Finally the default hashtable does
not allow duplicate objects, that is since the hash function will produce the very
same hash value again and if there is no way to tell two identical objects apart,
how will the computer do then? Adding two "John Smith" objects will not
be good, but maybe there are two such persons but they have different addresses,
birth date etc., that can be used by the hash function too.
Or, better, we have to follow
the rule that says that we should have an equals(Object)
method in your added object.
That is, we have to implement a method that can tell apart different objects, even
though they look alike, and return a boolean true or false. There is an equals(Object)
in the
Object class, but that can
only tell apart objects that are truly stored at different locations of your RAM,
it does not compare them on a more solid basis. Hence, if we by mistake make two
objects based on the same person, or whatever, they are considered not-equal by
that method, though they in real life are one.
put and get
Since mapping structures have that nice
performance they are used quite often. But the way to use them differs from the
previous structures that used a simple add(Object) method. First we have to implement the two
methods mentioned, hashCode and equals, both described in the
Object class. (Sometimes
the methods of Object is
sufficient, then we are done.)
Unfortunately the description on hashCode does
not tell the range of the int to return. Do not worry, any valid integer is okay.
The hard thing with hashCode is to find out how to equitable spread out the result.
The best case is when two distinct objects, differing only by a fraction, are not
given hash values close to each other (guess if there is much toil spent on finding
good hash functions). Given the hash value the table will compute it into an appropriate
index based on the tables actual size and the load factor wished, and finally add
the object somewhere in the array.
The equals(Object)
method is still the heart
of the hash table functionality. It is up to us to decide the basis for equality.
If we are sure that no two objects will be instantiated from the same source (e.g.
a person), we can rely on the Object class. Else we have to think about how to
tell objects apart, and return a true or false.
Next step is described in the code
below. Notice that we do not make any use of the
hashCode or equals methods,
but the table does. Since the Java Hashtable follows the Map interface we use the two methods put and get for add and indexAt.
...
Hashtable myTable = new Hashtable();
String addObj = new String("Alpha");
myTable.put(addObj, addObj);
addObj = new String("Beta");
myTable.put("Beta", addObj);
myTable.put("one", new Integer(1));
Integer tmpInt = (Integer)myTable.get("one");
String tmpStr = (String)myTable.get("Alpha");
|
|
Note that
put needs two objects, the
key and the value to be stored. Many times the key and the value are the very same
object, the object maps to itself. That is not necessary of course, as the Integer example
shows, the only way to get to the integer object is to give the key "one".
That is, the key to "James Bond" may be "Agent 007", no other
key will ever reveal the name of that spy.
With String the
equals does a compare character
by character and does not pay any attention to where the
String objects actually
are stored in memory. Thus you can get to a value by, for example another "Alpha"
that in fact is a new String object, but still gives the same hash value and equals
very well. If, on the contrary, the Integer object were put with itself as a key, we need
to have it on hand to get it out later and that is not what we liked to. Hence a
good practice with your classes may be a good equals
method, or a good toString that
produces a known key that you may replicate later on, without need to keep it on
hand.
A very, very simple test case.
At least at my computer I found that some of the latter strings
produce exactly the same hash value, maybe a flaw in the
hashCode implementation with very long strings, as the
latter strings came to be. Else we understand that the strings produce a hash value
that is later used by put to
insert the strings at their indexes in the hash table array.
We can not get the exact length of that array in the end, but
I guess it might be 47 since the default size is 11 (primes gives better result
than other sizes) and the default load factor is 0.75. Hence two turns in rehash have to be done, each does size * 2 + 1. This
time we waste more than 50% of the memory foot print, since it was only two or three
elements added after the latest rehash, but there is room for 15 elements until
the next rehash.
Summary
Previous installments
|
Into
Java, XI
|
Into
Java, XII
|
Into
Java, IX
|
Into
Java, X
|
Into
Java, VII
|
Into
Java, VIII
|
Into
Java, V
|
Into
Java, VI
|
Into
Java, III
|
Into
Java, IV
|
Into
Java, I
|
Into
Java, II
|
|
We have made a deep and much theoretical
dive into the field of data structures. The outcome will be that we have to think
twice when we are to chose a structure. Is the look-up time important, or is sortability
more important? Is duplicate elements to expect, or should they not be allowed?
How limited is the working memory?
The main difference between ordinary
arrays and list on the one hand, and maps on the other hand is that the former use
an index to get to an element, the latter use the key-value concept.
We will use many of the discussed
structures in the future and the next time we will start a slow wandering through
streams, reading and writing. And continuing this shock start on data structures,
but only one or two types at a time.
Thanks for this time and CU around.
Note:
This columns covers some classes only found in Java 2 or later, some others are
also found in Java 1.1.8. The theory holds for anyone.
Also note that Collections (with
a trailing s) is the name of the framework, but Collection
is an interface found in
the java.util package.
[ Go back ]

 Simon Gronlund is earning his
Master of Science in Computer Science at the Royal Institute of Technology, Sweden,
as an adult student. He also teaches Java and computer-related courses at the college.
When he isn't tampering with his Warp 4 PC, he spends his spare time with his two
boys and his wife.
Simon Gronlund is earning his
Master of Science in Computer Science at the Royal Institute of Technology, Sweden,
as an adult student. He also teaches Java and computer-related courses at the college.
When he isn't tampering with his Warp 4 PC, he spends his spare time with his two
boys and his wife.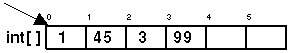 An array is simply several
variables in a row, the compiler fixed some kind of code that orders a line of consecutive
variables as seen in the image and the OS manages that. The advantage from this
is that now we only need one address that points to the beginning of the array,
held by the reference.
An array is simply several
variables in a row, the compiler fixed some kind of code that orders a line of consecutive
variables as seen in the image and the OS manages that. The advantage from this
is that now we only need one address that points to the beginning of the array,
held by the reference. The elements is found as the result
from add up the reference with the offset, the first element having zero offset.
Here is the reason why arrays, Vector and other data structures start at number
zero, the offset is zero at the first element. Hence we now can get to "99"
by adding 3 to the reference, as int answer = myIntArray[3] where myIntArray holds the reference.
The elements is found as the result
from add up the reference with the offset, the first element having zero offset.
Here is the reason why arrays, Vector and other data structures start at number
zero, the offset is zero at the first element. Hence we now can get to "99"
by adding 3 to the reference, as int answer = myIntArray[3] where myIntArray holds the reference. Else, normal actions on simple arrays
are performed efficiently and with no hassle. They are easily understood and not
hard to implement. Since Java hides the hazards with pointers and pointer arithmetic
the work is a breeze, as the add method show us in the left hand image. We simply keeps
track of the last index used and add the next element to the next index.
Else, normal actions on simple arrays
are performed efficiently and with no hassle. They are easily understood and not
hard to implement. Since Java hides the hazards with pointers and pointer arithmetic
the work is a breeze, as the add method show us in the left hand image. We simply keeps
track of the last index used and add the next element to the next index. Consider the left
part of the image, we remove the second element. Remove is clearly different from
assigning the second box another object, remove will leave an empty box, and empty
boxes, how would you like to keep track of them? You don't, you have to move every
element to the right of the empty box one step leftward. Again that is time consuming,
more time is spent the more leftward the removed element was located and the longer
the array is.
Consider the left
part of the image, we remove the second element. Remove is clearly different from
assigning the second box another object, remove will leave an empty box, and empty
boxes, how would you like to keep track of them? You don't, you have to move every
element to the right of the empty box one step leftward. Again that is time consuming,
more time is spent the more leftward the removed element was located and the longer
the array is. As the
problem with insert and remove came from the time spent on
arrayCopy, shuffling elements
left- or rightward, we would like a data structure that do not need these operations.
A linked list is the answer. Think of nodes linked, or chained, together as the
uppermost image part shows.
As the
problem with insert and remove came from the time spent on
arrayCopy, shuffling elements
left- or rightward, we would like a data structure that do not need these operations.
A linked list is the answer. Think of nodes linked, or chained, together as the
uppermost image part shows.
